This post is part of my What Is… series that explains spatial audio techniques and terminology.
OK, you know what stereo is. Everyone knows what stereo is. So why bother writing about it? Well, because it allows us to introduce some links between the reproduction system and spatial perception before moving on to systems which use much more than 2 loudspeakers.
Before going any further, this post will deal with amplitude panning. Time panning will be left for another day. I also won’t be covering stereo microphone recording techniques because that could fill up its own series of posts.
The Playback Setup
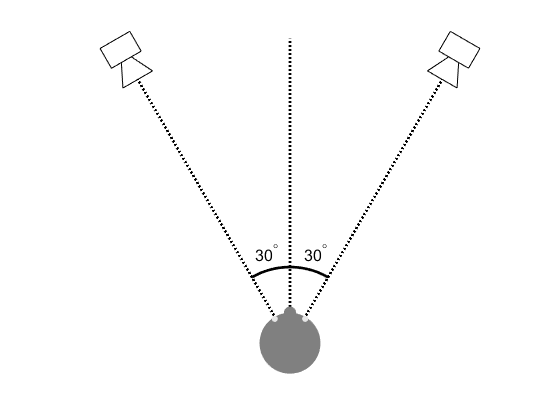
A standard stereo setup is two loudspeakers placed symmetrically at (pm30^{circ}) to the left and right of the listener. We will assume for now that there is only a single listener equidistant from both loudspeakers. The loudspeaker basis angle can be wider or narrower but if they get too wide there is a hole-in-the-middle problem. Too narrow and we reduce the range of positions at which the source can be placed. Placing the loudspeakers at (pm30^{circ}) gives a good compromise between these two, balancing sound image quality with potential soundstage width.

Placing the Sound
Amplitude panning takes a mono signal and sends copies to the two output channels with (potentially) different levels. When played back over two loudspeakers the level difference between the two channels controls the perceived direction of the sound source. With amplitude panning the perceived image will remain between the loudspeakers. If we know the level difference between the two channels then we can predict the perceived direction using a panning law. The two most famous of these are the tangent law and the sine law. The tangent law is defined as
begin{equation}
frac{tantheta}{tantheta_{0}} = frac{G_{L} – G_{R}}{G_{L} + G_{R}}
end{equation}
where (theta) is the source direction, (theta_0) is the angle between either loudspeaker and the front (30 degrees in the case illustrated above) and (G_{L}) and (G_{R}) are the linear gains of the left and right loudspeakers.
How It Works
Despite being simple conceptually and very common, the psychoacoustics of stereo are actually quite complex. We’ll stick to discussing how it relates to the main spatial hearing cues.
As long as both loudspeakers are active, signals from both loudspeakers will reach both ears. Due to the layout symmetry, both ears receive signals at the same time but with different intensities corresponding to the level differences of the loudspeakers. Furthermore, since it has further to travel, the signal from the left loudspeaker will reach the right ear slightly later than the signal from the right loudspeaker. The opposite is true for the right ear. This time difference combined with the intensity difference gives rise to interference that generates phase differences at the ears. These phase differences are interpreted as time differences, moving the sound between the loudspeakers.
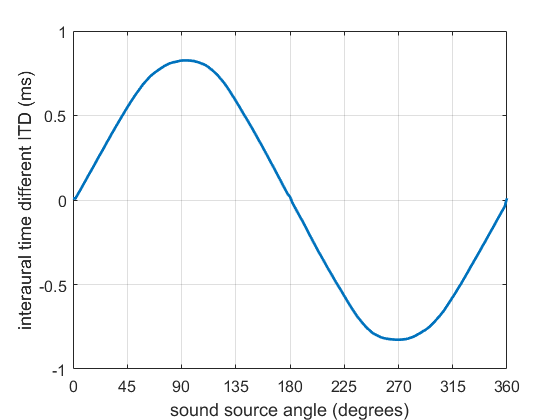
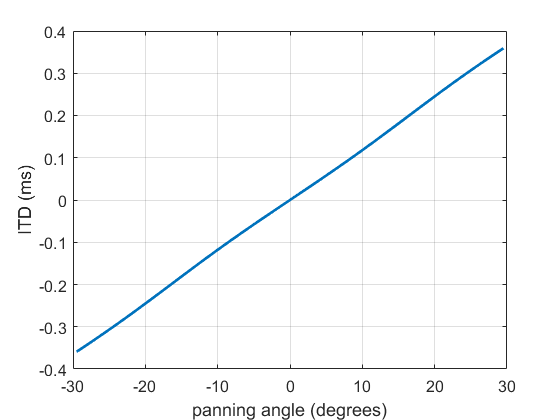
The ITD (below 1400 Hz) is shown in the figure and is roughly linear with panning angle. This is pretty close to exactly what we see for a real sound source moving between these angles. This works pretty well for loudspeakers at (pm30^{circ}) or less, but once the angle gets bigger the relationship becomes slightly less linear.
These strong, predictable ITD cues mean that any sound source with a decent amount of low frequency information will allow us to place the image pretty precisely. Content in higher frequency ranges won’t necessarily be in the same direction as long frequency content because ILD becomes the main cue.
Even though stereo gives rise to interaural differences that similar to those of a real source, that does not mean it is a physically-based spatial audio system (like HOA and WFS). The aim is to produce a psychoacoustically plausible (or at least pleasing) sound scene. Psychoacoustically-based spatial audio systems tend to use the loudspeakers available to fit some aim (precise image, broad source) without regards to if the resulting sound scene ressembles anything a real sound source would emit.
So, there you have a quick overview of stereo from a spatial audio perspective. There are other issues that will be cover later because they relate to other spatial audio techniques. For example, what if I’m not in the sweet spot? What if the speakers are to the side or I turn my head? What if I add a third (or forth or fifth) active loudspeaker? Why do some sounds panned to the centre sound elevated? All of these remaining and non-trivial points shows just how complex perception of even a simple spatial audio system can be.